Schwingung einer gespannten Saite mit fixierten Endpunkten
(Waves on a stretched string with fixed ends) 

>	restart:with(plots):

 

Warning, the name changecoords has been redefined 

Solution of wave equation: 

>	l := 1; c:=1;

 

Spatial solution 

>	X[n](x):= sin(n*Pi/l*x);X[m](x):=subs(n=m,X[n](x)):

 

Time-dependent solution   

>	T[n](t):= (A(n)*cos(n*Pi*c/l*t)+B(n)*sin(n*Pi*c/l*t));u[n](x,t):=T[n](t)*X[n](x):

 

Eigenfunction expansion  

>	u(x,t):=Sum(u[n](x,t),n=1..infinity);

 

Initial conditions 

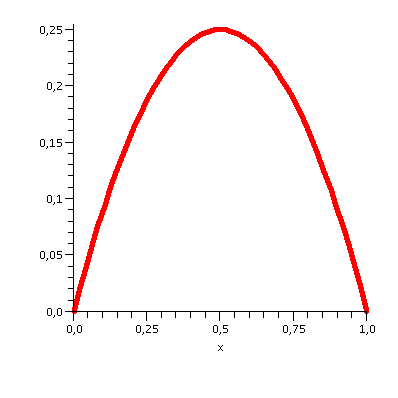
>	u0(x):=x*(1-x);

 

>	v(x):=x*(1-x);

 

Plot of u0: 

>	plot(u0(x) , x=0..l ,thickness=5);

 

Evaluation of coefficients for specific ICs 

>	A(n):=(2/l)*Int(u0(x)*X[n](x) ,x=0..l);A(n):=expand(value(%)):

 

>	A(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},A(n)));

 

>	B(n):=(2/(n*Pi*c))*Int( v(x)*X[n](x),x=0...l);B(n):=expand(value(%)):

 

>	B(n):=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},%));

 

(Observe convergence of series.) 

>	u[n](x,t):=eval(T[n](t)*X[n](x)):

 

Series solution  

>	u(x,t):=Sum(u[n](x,t),n=1..infinity);

 

First few terms of sum  

>	u(x,t):=sum(u[n](x,t),n=1..5);

 

Animation 

>	animate(u(x,t),x=0...l,t=0..20,color=red,thickness=5 , frames=600 );